Is Really 0.999… = 1?

You might have heard the statement that 0.999… = 1 and probably you thought nah, not true. In this post we are gonna dive deep into the statement and give to the non mathematician reader a convicing explanation and proof why ii is true.

First, what is the number 0.999…?

Simply is the number with infinite number of 9s to the right. Obviously 0.999… = 0.9999…. = 0.99999… and so on. They all represent the same number

If you previously investigated in this matter you may have found a proof like this:

1 = 3 \cdot {1}/3 = 3  \cdot 0.333... = 0.999... 

This is perfectly fine but in my opinion it gives no insight as to why 0.999… is 1 and it seems some kind of magic algebraic manipulation.

What means one number to equal another one?

One way to think about one number being equal to another is that they are arbitrarily close. Ie. they are as close as we want them to be.

For instance 2-1 = 1 and so the number 2 and 1 have a «distance» of 1.

The way to express mathematically that two numbers are arbitrarily close is the following:

Imagine if for any real positive number Epsilon we can find that the numbers 1 and 0.999… are closer than Epsilon then 1 and 0.999… are arbitrarily close and thus they are equal.

Let’s go for the proof:

We will go step by a step and the give it complete:

note first that 1-0.9 = 0.1 = 1/10

1-0.99 = 0.01 = 1/100 and so on.

We can now give the proof:

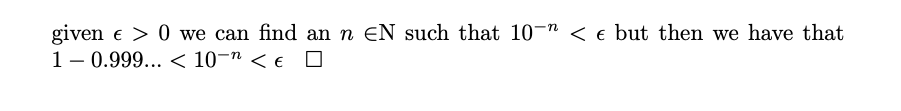
The reason it’s hard for us to grasp how can 0.999… = 1 is because the number 0.999… is a number that we can’t really imagine in a concrete way because it involves an infinite process. Humans don’t have the capacity to think about infinity. Or infinity is just something to big for our comprehension. Still mathematics developed techniques that help us understand some infinite processes better. In this case we used analysis techniques that helped us to prove it.