The secretary problem also known as the marriage problem is a famous riddle of decision making. The problem can be formulated as follows:
«You are the interviewer that wants to select a new secretary. You know that n possible secretaries will come and you will interview them one by one. After each interview you should take the decision of choose him/her. If you don’t choose any then you will get the last one. The problem is to define the best strategy that maximizes the probability of choosing the best candidate»
You can think on the riddle on your own, from this point you will find SPOILERS about it.
A first thought about the problem, obviously if we choose at random one of the candidates the chances are 1/n of choosing the best one. As n increases this goes to zero.
The question is can we find a better strategy? If so, how much better can it be made?
You may want to think about this, but the answer is yes and actually we can find a strategy which makes the probability never goes under 30%.
Solution
The solution is based in a stopping rule, from the n applicants we choose some r < n. Then the first r applicants will be discarded and used to compare with the following ones. Then the next one that comes and is better than the first r will be the chosen one.
Let’s see it with an example:
With n=4 and r=2 we have:
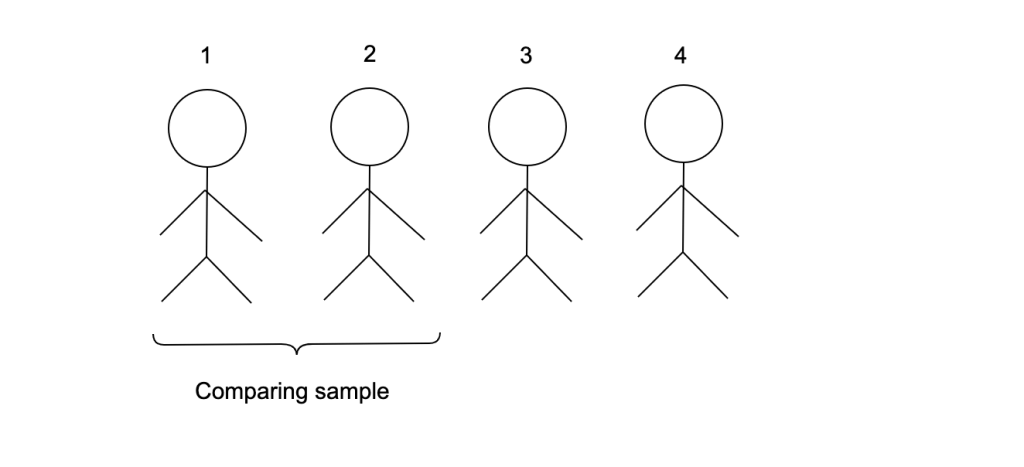
Then after we evaluate the 1 and 2nd and we see how good they are the third comes and if he was better was better than 1 and 2nd he’s chosen.

Then what happens if the best one was the 4th?

Of course if the best one was the first or second then the chances are 0 of choosing them. All in all the probability of choosing the best candidate is:
P_4^2 = \frac{1}{4} + \frac{1}{4} \cdot \frac{2}{3} = \frac{5}{12} = 0.4166..We can do the same but with r = 1, I can leave that process to you. you should get that in that case the probability is 0.458.
For each n there’s an r that maximizes the probability. For the mathematician reader you can find the proof of it at the bottom of the entry.
For example for n=4 is r=1 and for n=8 we have r=3.
What can be shown is that with this strategy the probability as we get more applicants, the probability of choosing the best is bounded and never goes below 1/e = 0.36 !
Ofcourse the problem formulation is really constrained and a real life scenario like this it’s highly utopic. Usually you can just call the first after all of them if you felt he/she was the first. Nevertheless I think the problem solution is pretty elegant and highlights that sometimes things can be approached in clever ways and they deliver quite better outcomes than without any thinking on them. A probability of at least 0.36.. no matter the number of applicants is high and not what one thinks when he is first presented the problem.
For the more maths oriented reader you can read in the following pdf the problem approached in a formal way and the derivation of the results commented above.
Why is this the best strategy?
You might think that proving this to be the best strategy might be hard to prove but actually it is quite the contrary.
If from the n candidates we choose say the candidate i and he/she was better than the i-1 before candidates we can can say that the bigger the i the more probable is that we have chosen the best candidate.
Mathematically it means that if the i candidate is the best we have seen so far the chances that he/she is the best one are i/n (the probability that the best one is in the i-first candidates).
Then i/n is an increasing function of i and so it means that the latter is found this i best candidate the better chances we find that he/she is the best. So the optimal policy lies in the family of policies we have considered from the n candidates discard some r-first candidates and then the first one that comes shall be chosen.
Questions for you
Writing this post and going through the problem carefully has left me with some questions, you can leave me in the comments your thoughts about them:
- As we have seen the r should be the one in which r/n is around 1/e. This doesn’t mean thought, that it should be the closest. n=10 is an example of this. Is there any result on this?
- We have also seen that the probability tends to 1/e as we tend n to infinity and we choose r such that r/n=1/e. Can it happen that when we choose the r the probability goes below of 1/e for some n?